Что значит параболическая антенна

Спутниковые параболические антенны: свойства, особенности, принцип работы

Что такое параболическая спутниковая антенна

Конструкция параболической спутниковой тарелки

Зеркало такой антенны обладает изогнутой поверхностью с имеющим форму параболы поперечным сечением, собирает попадающие на него радиоволны в своем фокусе, где установлен облучатель.

Рефлектор тарелки изготавливается из материала, обладающего хорошей электрической проводимостью (алюминиевые сплавы, сталь), имеющего антикоррозионное покрытие. Также зеркало может быть выполнено из неметаллических материалов, таких, как пластмасса, углепластик, стеклопластик.

Конструкция антенны также предполагает наличие опорно-поворотного устройства (ОПУ), моторизованного или имеющего ручное управление, осуществляющего наведение системы на спутник, а также обеспечивающего стабильное положение тарелки. При работе в неблагоприятных климатических условиях конструкция может быть снабжена системой антиобледенения, представленной тепловыми пушками или нагревательными элементами.

Математическое обоснование эффективности параболических антенн

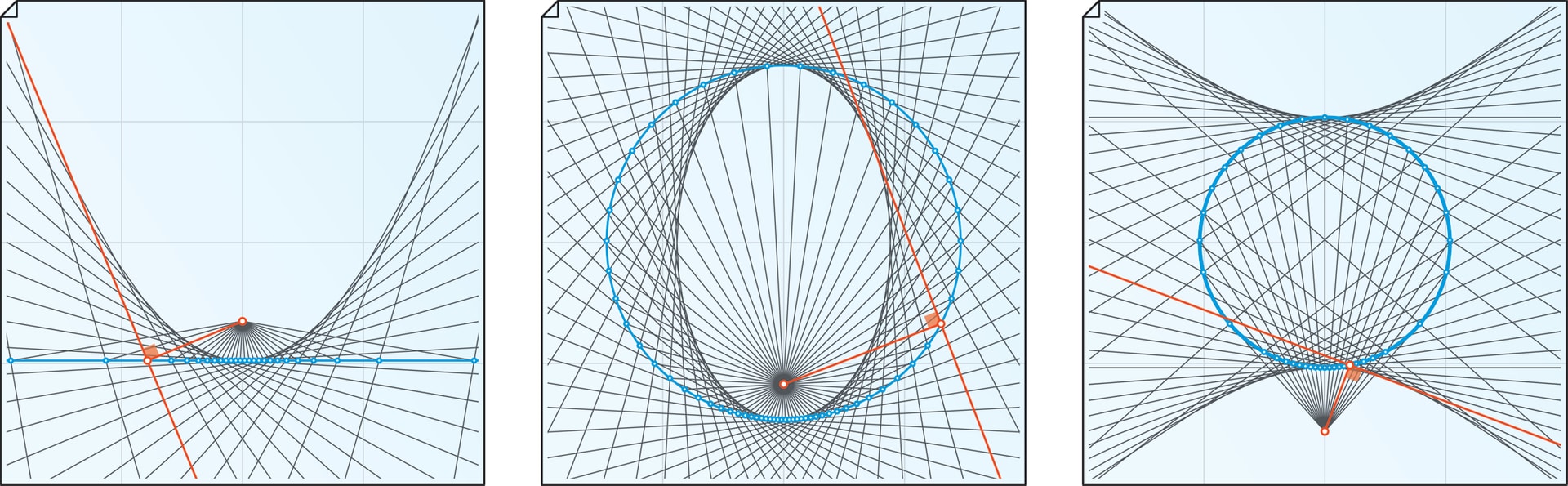
Параболой называется геометрическое место точек, удаленных на одинаковое расстояние от называемой директрисой прямой и от точки, не лежащей на ней (фокуса).

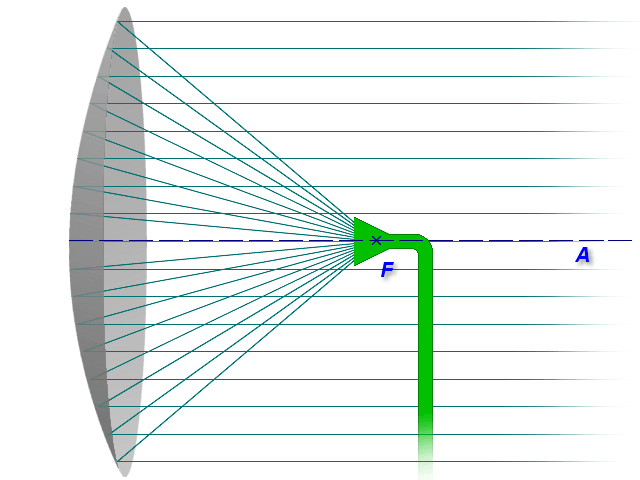
Параболу отражает график функции: y = ax2+bx+c. Ее оптические свойства заключаются в следующем: лучи, отражающиеся от помещенного в фокус параболы точечного источника света, будут перемещаться по оси симметрии параболы, а передний фронт будет проходить перпендикулярно этой оси. Если же на параболу попадает пучок параллельных оси симметрии лучей, то они одновременно придут к фокусу, отразившись от параболы, если передний фронт потока проходит перпендикулярно оси.

По этому же принципу построена работа параболического отражателя: при расположении излучателя в фокусе, отраженные от поверхности зеркала лучи будут двигаться параллельно оси вращения параболоида. Также при попадании на него лучей, параллельных оси, они собираются в фокусе.

Виды параболических спутниковых тарелок

Прямофокусная параболическая антенна

Зеркало такой тарелки симметрично, а фокус его находится на оси симметрии. Перед зеркалом в точке фокусировки расположен облучатель. Применяются также схемы с двумя зеркалами, уменьшающие шумовую температуру, размеры антенны, однако расчет их сложен, как и изготовление с последующей настройкой.

Прямофокусная тарелка позволяет задействовать около 90% полезной площади, что важно для бесперебойного приема спутникового сигнала. Однако конструкция имеет форму чаши, где легко скапливаются осадки, а конвертер может затенять полезную площадь, что приводит к снижению эффективности. Поэтому прямофокусная схема применяется для антенн большого диаметра (от 1.5−2 метров).

Офсетная параболическая тарелка

Представлена асимметричной вырезкой из параболоида вращения. Имеет смещенный в сторону от центра облучатель, где диаграмма направленности также «сдвинута» относительно оси отражателя на угол смещения (или офсета).

Зеркало овальной формы расположено почти вертикально или направлено вниз, а облучатель, установленный ниже центра тяжести тарелки, увеличивает сопротивление ветровым нагрузкам. Также устройства подобного типа могут принимать спутниковый сигнал большей мощности, компактны, просты в установке, не собирают осадки благодаря тому, что направлены вниз. Однако конвертер таких антенн открыт и подвергается воздействию влаги, поэтому требует дополнительной защиты.

Антенна Кассегрена

Представлена системой зеркал, имеющих двойное отражение, основанной на принципах работы оптического телескопа Кассегрена. Конструкцию составляют главное параболическое зеркало и дополнительное гиперболическое зеркало. Один из двойных гиперболических фокусов находится в фокусе всей системы по центру излучателя, другой — в фокусе параболы. Источник питания находится на антенне или позади, освещая вторичное зеркало в фокусе. Отражаясь от гиперболического зеркала, лучи идут к основному рефлектору, который снова отражает их вперед, что формирует выходящий луч.

Антенна Кассегрена широко распространена для функционирования в миллиметровом волновом диапазоне. Не требует подвешивания фидера перед зеркалом. Используется системами связи, работающими по типу «точка-точка», благодаря суженной диаграмме направленности, высокому коэффициенту усиления, а также системами спутниковой связи, радарами. Подобные тарелки экономически выгодны, имеют небольшие размеры, допускают различное размещение излучателя.

Источник

Основы радиолокации

Параболическая антенна

Рисунок 1. Принцип действия параболической зеркальной антенны

Рисунок 1. Принцип действия параболической зеркальной антенны

Параболическая антенна

Параболический отражатель , параболическая антенна, зеркальная антенна — это устройство, используемое для сбора или фокусировки энергии такой как, например, энергия электромагнитной волны. Плоские волны, падающие на такую антенну с направления, параллельного оси параболоида, преобразовываются в сферическую волну и фокусируются в точке, где находится фокус параболоида. И наоборот, сферическая выолна, излучаемая облучателем, расположенным в фокусе параболоида, отражаясь от его поверхности, преобразуется в плоскую волну, распространяющуюся вдоль оси симметрии зеркала.

Параболическая антенна, напоминающая своей формой тарелку, является одной из наиболее часто используемых в различных радиолокационных приложениях. На Рисунке 1 схематически изображена параболическая антенна. Такая антенна имеет в своем составе круговой параболический отражатель (зеркало) и точечный источник, расположенный в фокусе отражателя. Этот точечный источник называют облучателем, иногда — первичным излучателем.

Круговой параболический отражатель (параболоид) представляет собой конструкцию из металла, как правило, в виде каркаса (рамы), покрытого металлической сеткой с внутренней стороны. Для обеспечения требуемого отражения от зеркала размер ячейки сетки должен быть менее λ/ 10. Такое металлическая сетка работает как зеркало для электромагнитной энергии.

Для этого типа рефлектора, в соответствии с законами оптики и аналитической геометрии, все отраженные лучи будут параллельны оси параболоида, что, в идеале, означает формирование одного луча антенны, параллельного главной оси, без боковых лепестков. Поле, излучаемое рупорным облучателем, имеет сферический фронт. Волна, достигшая рефлектора и отразившаяся от него, меняет свою фазу на 180°. Угол отражения волны равен углу ее падения на рефлектор и поэтому после отражения все лучи будут параллельны.

На Рисунке 2 изображена идеализированная радиолокационная антенна в форме параболоида вращения, формирующая игольчатый луч (луч карандашного типа). Если отражатель имеет эллиптическую форму, то формируемый им луч будет иметь веерную форму. Поверхности антенн обзорных радиолокаторов имеют разную кривизну в горизонтальной и верткальной плоскостях, чем достигается требуемая ширина диаграммы направленности в азимутальной плоскости (игольчатый луч) и классическая косекансквадратная веерная диаграмма направленности по углу места.

Рисунок 2. Диаграмма излучения параболоида

Рисунок 2. Диаграмма излучения параболоида

Рисунок 2. Диаграмма излучения параболоида

Однако на практике невозможно достичь идельного результата, такого, как представлен на Рисунке 1. Диаграммы направленности реальных параболических антенн имеют коническую форму из-за неровностей поверхности рефлектора, возникающих при его изготовлении. Ширина основного лепестка может меняться от 1 … 2 градусов для одних радиолокаторов до 15 … 20 градусов для других.

Рисунок 3. Горизонтальное сечение реально измеренной диаграммы излучения параболической антенны в логарифмическом масштабе, измеренной при полевом эксперименте

Диаграмма рассеяния параболической антенны имеет в своем составе основной лепесток, направленный вдоль оси распространения волны, и несколько небольших боковых лепестков. При использовании рефлекторов такого типа возможно формирование очень узких лучей.

Коэффициент усиления антенны с параболическим отражателем может быть рассчитан следующим образом.

• Θ_Az — ширина луча в азимутальной плоскости;
• Θ_El — ширина луча в угломестной плоскости.

Это приближенная формула, но дает хорошую оценку для большинства задач и поясняет взаимосвязь коэффициента усиления антенны и ширины ее диаграммы направленности.

Рисунок 3. Горизонтальное сечение реально измеренной диаграммы излучения параболической антенны в логарифмическом масштабе, измеренной при полевом эксперименте

Рисунок 4. Трехмерная диаграмма излучения параболической антенны, определенная путем математического моделирования

Рисунок 4. Трехмерная диаграмма излучения параболической антенны, определенная путем математического моделирования

Рисунок 4. Трехмерная диаграмма излучения параболической антенны, определенная путем математического моделирования

Обратите внимание: разница между Рисунком 2 и Рисунком 4 имеет следующий смысл. На Рисунке 2 дальность (продольная координата) откладывается в линейном масштабе, поэтому боковые лепестки не видны. На Рисунке 4 дальность откладывается в логарифмическом масштабе, поэтому боковые лепестки становятся видны, а верхушка главного лепестка приплюснута

Параболические антенны одинарной и двойной кривизны

Рисунок 5. Сравнение отражателей с поверхностями одинарной кривизны и двойной кривизны

Рисунок 5. Сравнение отражателей с поверхностями одинарной кривизны и двойной кривизны

Для поверхности одинарной кривизны или двумерного рефлектора вместо фокальной точки (фокуса) имеет место фокальная линия. Форму параболы имеет кромка такой поверхности, а сдвигая эту линию вдоль образующей, получаем форму всего рефлектора. Антенна радиолокатора Тип 1022 является примером такого типа дсумерного рефлектора.

Поверхность двойной кривизны или трехмерный рефлектор получается вращением параболы вокруг своей оси. В данном случае парабола будет наблюдаться с любого направления.

Издатель: Кристиан Вольф, Автор: Андрій Музиченко
Текст доступен на условиях лицензий: GNU Free Documentation License
а также Creative Commons Attribution-Share Alike 3.0 Unported License,
могут применяться дополнительные условия.
(Онлайн с ноября 1998 года)

Источник

‍ Параболическая антенна

Работа спут­ни­ко­вых антенн, в част­но­сти тех, кото­рые при­нимают теле­ви­зи­он­ный сиг­нал, осно­вана на опти­че­ском свойстве пара­болы.

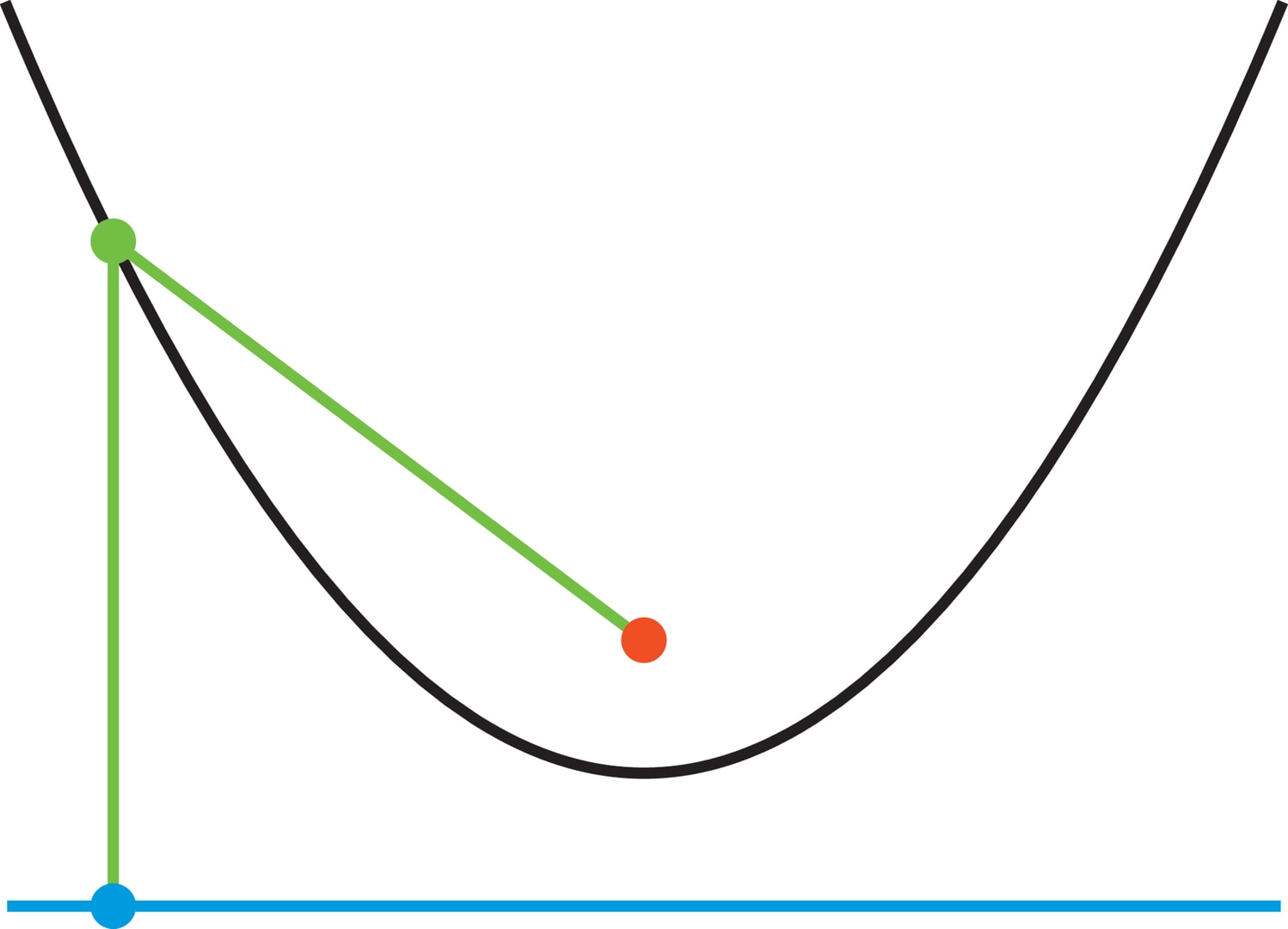
Пара­бола — это геомет­ри­че­ское место точек, рав­но­уда­лён­ных от прямой (назы­ва­емой дирек­три­сой) и от не лежащей на дирек­трисе точки (назы­ва­емой фоку­сом). Из при­ве­дён­ного опре­де­ле­ния пара­болы несложно полу­чить «школь­ное»: пара­бола — это график квад­ра­тич­ной функции $y=ax^2+bx+c$ (в част­но­сти, $y=x^2$) .

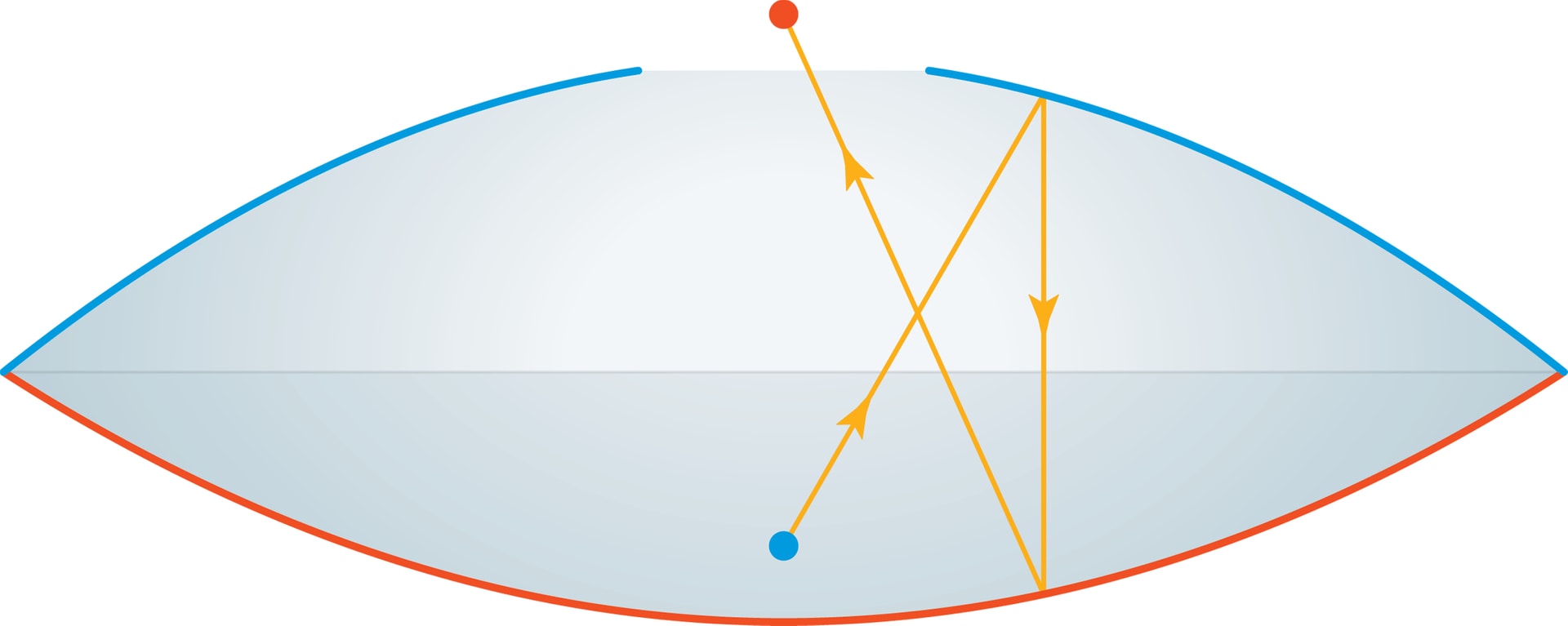
Сформу­ли­руем упомя­ну­тое опти­че­ское свойство пара­болы. Если в фокусе пара­болы поме­стить точеч­ный источ­ник света (лампочку) и вклю­чить его, то лучи, отра­зившись от пара­болы, пой­дут парал­лельно оси симмет­рии пара­болы, при­чём перед­ний фронт будет перпен­ди­ку­ля­рен оси.

Верно и обрат­ное — если на пара­болу падает поток лучей, парал­лель­ных оси симмет­рии, то, отра­зившись от пара­болы, лучи при­дут в фокус; при­чём при­дут одно­временно, если перед­ний фронт потока лучей перпен­ди­ку­ля­рен оси.

При враще­нии пара­болы вокруг её оси симмет­рии полу­ча­ется пара­бо­лоид враще­ния — поверх­ность вто­рого порядка.

При любом сече­нии пара­бо­ло­ида плос­ко­стями, про­хо­дящими через ось симмет­рии, полу­чаются рав­ные пара­болы с общим фоку­сом, поэтому пара­бо­лоид тоже обла­дает опти­че­ским свойством. Если поме­стить излу­ча­тель в фокус, то лучи, отра­зившись от поверх­но­сти, пой­дут парал­лельно оси враще­ния. А если на пара­бо­лоид падают лучи, парал­лель­ные его оси, то после отраже­ния все они соби­раются в фокусе.

Опти­че­ское свойство — принци­пи­аль­ная основа пара­бо­ли­че­ских антенн.

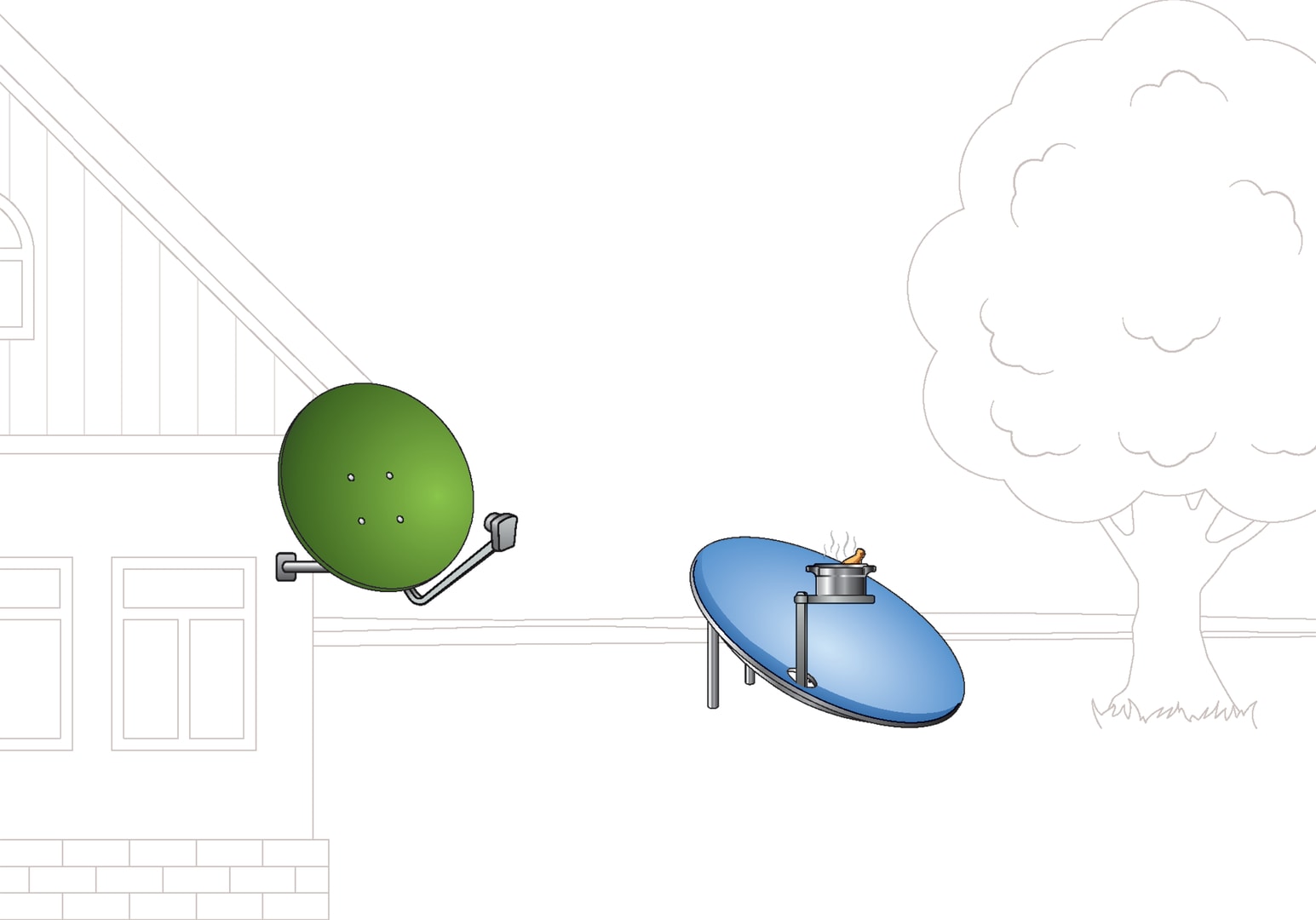
Антенны могут вращаться, при­мер — пара­бо­ли­че­ские антенны в аэропор­тах, по форме являющи­еся «лом­ти­ками» огром­ных пара­бо­ло­и­дов; они и пере­дают, и при­нимают сиг­нал. Антенны могут быть непо­движ­ными. К послед­нему типу отно­сятся быто­вые спут­ни­ко­вые теле­ви­зи­он­ные антенны («тарелки»): их наце­ли­вают на спут­ник-ретранс­ля­тор, нахо­дящийся высоко над Зем­лёй на гео­стаци­о­нар­ной орбите, после чего их положе­ние фик­си­ру­ется. Поскольку спут­ник нахо­дится далеко от поверх­но­сти, при­хо­дящие от него лучи в точке при­ёма антен­ной можно счи­тать парал­лель­ными. В фокусе спут­ни­ко­вой антенны нахо­дится при­ём­ник, от кото­рого сиг­нал по кабелю отправ­ля­ется к теле­ви­зору.

Эта же идея при­ме­ня­ется при созда­нии про­жек­то­ров желез­но­до­рож­ных локо­мо­ти­вов, фар автомо­би­лей, её можно исполь­зо­вать даже для при­го­тов­ле­ния еды в поле­вых усло­виях.

Опти­че­ское свойство пара­болы «знает» и мир живой при­роды. Напри­мер, неко­то­рые север­ные цветы, живущие в усло­виях корот­кого лета и недо­статка сол­неч­ных лучей, рас­кры­вают лепестки в форме пара­бо­ло­ида, чтобы «сердцу» цветка было теп­лее.

Разворот книги

Допол­не­ния, коммен­та­рии

Древ­ние греки занима­лись изу­че­нием эллипса, гипер­болы и пара­болы, рас­смат­ри­вая их как кони­че­ские сече­ния. Апол­ло­ний (262 до н. э. — 190 до н. э., родом из Перги, но рабо­тавший в Алек­сан­дрии, современ­ник Архимеда) напи­сал труд «Кони­че­ские сече­ния» в восьми книгах, поло­вина из кото­рых дошла до наших дней только в сред­не­ве­ко­вых араб­ских пере­во­дах.

Апол­ло­ний рас­смат­ри­вал фокусы эллипса и гипер­болы, хотя у него и не было спе­ци­аль­ного термина для этих точек, знал их свойства, вклю­чая опти­че­ские.

Диокл, млад­ший современ­ник Апол­ло­ния, в сочи­не­нии «О зажига­тель­ных зер­ка­лах» при­во­дит опти­че­ское свойство пара­болы, видимо, осно­вы­ва­ясь на результа­тах учё­ных круга Архимеда. Это сочи­не­ние также сохра­ни­лось лишь благо­даря араб­ским пере­во­дам, в кото­рых пара­бо­лоид враще­ния назы­вался «зажига­тель­ным зер­ка­лом», а фокус пара­болы — «местом зажига­ния».

При изда­нии латин­ских пере­во­дов араб­ских матема­ти­че­ских тек­стов «место зажига­ния» не могло не пре­вра­титься в латин­ское focus — «очаг, огонь». Как термин «фокус» был вве­дён Иоган­ном Кепле­ром в сочи­не­нии «Опти­че­ская часть аст­ро­номии» («Astronomiae pars optica», 1604), при­чём не только для пара­болы, но и для эллипса и гипер­болы.

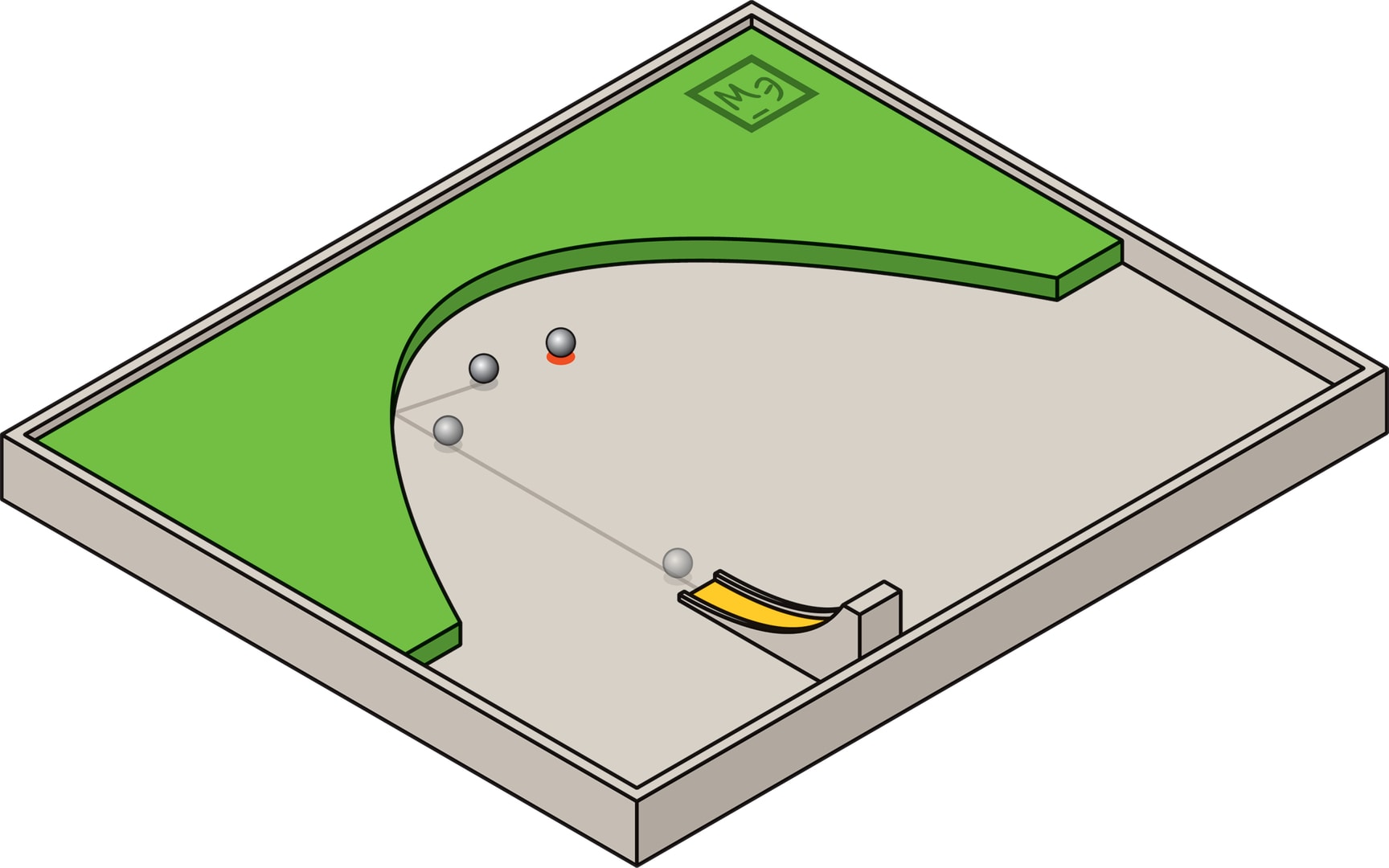
Опти­че­ское свойство пара­болы пред­ста­нет как экс­пе­римен­таль­ный факт, если изго­то­вить

В этой модели изогну­тый бор­тик пред­став­ляет пара­болу, на сукне отме­чен фокус — точка, в кото­рую надо поста­вить шарик-мишень. Основ­ной шарик будет ска­ты­ваться с подвиж­ной горки, кото­рую все­гда размещают так, чтобы направ­ле­ние ска­ты­вающегося шарика было парал­лельно оси пара­болы (напри­мер, можно сдвигать горку вдоль прямой стенки бильярда, рас­по­ложен­ной перпен­ди­ку­лярно оси пара­болы). Шарик, ска­ты­ва­ясь с горки, после отраже­ния от бор­тика все­гда будет попа­дать в шарик, размещён­ный в фокусе пара­болы!

При само­сто­я­тель­ном изго­тов­ле­нии модели сле­дует учесть, что бор­тик — это экви­ди­станта пара­болы, её сдвиг в каж­дой точке по нормали к пара­боле на рас­сто­я­ние, рав­ное ради­усу шарика (в иде­аль­ной геомет­ри­че­ской модели от пара­болы отража­ется центр шарика, точка). Радиус шарика должен быть не слиш­ком мал, чтобы сглажи­вать возмож­ные погреш­но­сти.

Каче­ство изго­тов­лен­ной модели можно оце­нить, если про­ве­сти экс­пе­римент, убрав шарик-мишень. Ска­ты­вающийся с горки шарик после пер­вого отраже­ния от бор­тика должен пройти через отме­чен­ный фокус, а после вто­рого — пока­титься парал­лельно оси пара­болы.

Геомет­ри­че­ское опре­де­ле­ние поз­во­ляет

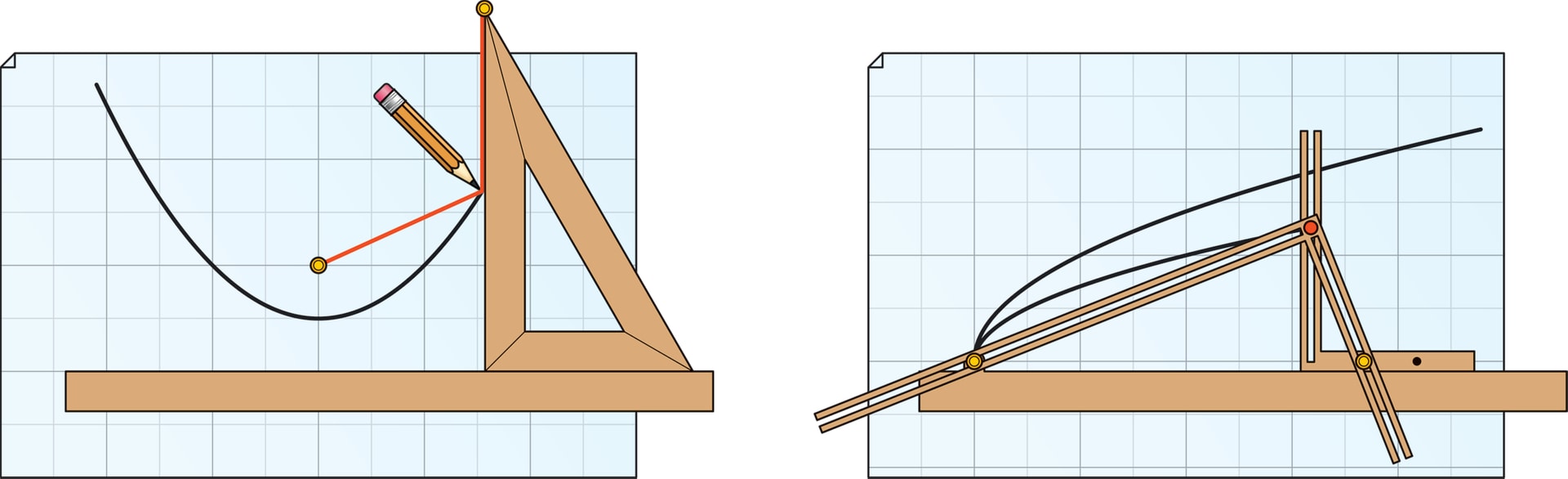
⁠ нари­со­вать пара­болу с дан­ным фоку­сом и дан­ной дирек­три­сой.

Вдоль дирек­трисы положим линейку, в фокусе кноп­кой закрепим конец нити. Вто­рой конец нити закреп­ля­ется в вершине уголь­ника, катет кото­рого при­ложен к линейке. Если при­жать нить ко вто­рому катету каран­дашом, сохра­няя её натя­ну­той при скольже­нии уголь­ника вдоль линейки, то про­ве­дён­ная линия будет пара­бо­лой.

Устройства, вычер­чи­вающие пара­болы, назы­ваются пара­бо­лографами. Изящ­ную

⁠ кон­струкцию при­думал в XVII веке ита­льян­ский матема­тик Бона­вен­тура Кава­льери (извест­ный как пред­ше­ствен­ник созда­те­лей интеграль­ного исчис­ле­ния).

Устройство состоит из трёх свя­зан­ных дета­лей: непо­движ­ной отно­си­тельно листа линейки (гори­зон­таль) и двух жёст­ких прямых углов. У пер­вого угла гори­зон­таль­ная сто­рона сколь­зит вдоль линейки, а по его вер­ти­каль­ной сто­роне сколь­зит вершина (с грифе­лем) вто­рого угла. При этом в каж­дый момент времени сто­роны вто­рого угла про­хо­дят через штифты: один закреп­лён на непо­движ­ной линейке, а дру­гой — на гори­зон­таль­ной сто­роне подвиж­ного угла.

То, что линия, про­ве­дён­ная грифе­лем, будет пара­бо­лой, сле­дует из извест­ного свойства прямо­уголь­ного тре­уголь­ника: квад­рат длины высоты, опущен­ной на гипо­те­нузу, равен про­из­ве­де­нию длин отрез­ков, на кото­рые её делит высота. Параметр пара­болы регу­ли­ру­ется перемеще­нием штифта на гори­зон­таль­ной сто­роне пер­вого угла.

⁠ «изго­то­вить» , про­ведя серию опытов с бумаж­ным листом — в результате вы полу­чите не нари­со­ван­ную, но «видимую» линию, кото­рой касаются много­чис­лен­ные прямые.

На листе бумаги нари­суйте прямую и отметьте точку, не лежащую на этой прямой (фокус будущей пара­болы). Через выбран­ную точку на прямой про­ве­дите перпен­ди­ку­ляр к отрезку, соеди­няющему эту точку с отме­чен­ной. Перпен­ди­ку­ляр можно даже не про­во­дить каран­дашом, а опре­де­лить на глаз и перегнуть по нему лист бумаги. Про­де­лав проце­дуру для нескольких точек на прямой, вы уви­дите пара­болу, как гра­ницу обла­сти, «окружён­ной» лини­ями сгиба.

Как оги­бающую семейства линий (см. Бол­тян­ский В. Г. «Оги­бающая») можно полу­чить и другие кони­че­ские сече­ния (см. коммен­та­рий к ста­тье ⁠ «Шухов­ские башни» ), только вме­сто началь­ной прямой нужно взять окруж­ность. Если точка (фокус) внутри окруж­но­сти, то полу­чится

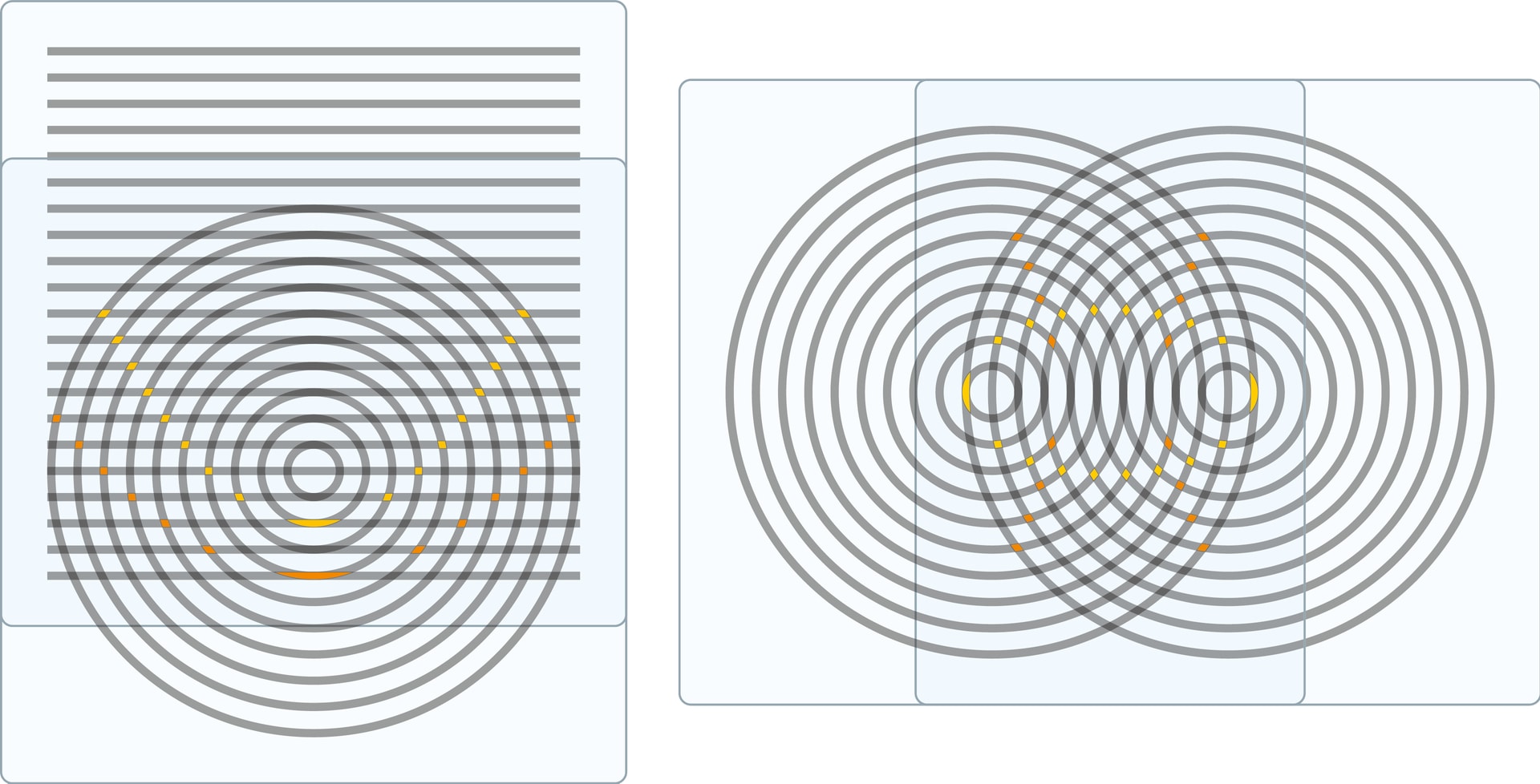
Все кони­че­ские сече­ния (эллипс, пара­болу, гипер­болу) можно полу­чить в виде муара — допол­ни­тель­ного геомет­ри­че­ского узора, обра­зующегося при наложе­нии двух изоб­раже­ний. Возьмите «про­зрачку» и на прин­тере напе­ча­тайте прямо­ли­ней­ные полоски на фик­си­ро­ван­ном рас­сто­я­нии между сосед­ними. На другом листе напе­ча­тайте круго­вые полоски (концен­три­че­ские окруж­но­сти) той же ширины и с тем же рас­сто­я­нием между сосед­ними.

Если наложить эти листы друг на друга так, чтобы одна из прямых про­хо­дила через центр окруж­но­стей, то вы уви­дите семейство пара­бол. А если наложить две оди­на­ко­вые «круго­вые» про­зрачки так, чтобы рас­сто­я­ние между цен­трами кругов было кратно рас­сто­я­нию между окруж­но­стями, то можно уви­деть эллипсы и пере­се­кающие их гипер­болы.

Чита­тель мог встре­чать впе­чат­ляющую игрушку: на крышке «летающей тарелки» вы видите объект, ося­за­емо-объём­ный, пыта­е­тесь его взять, и… пальцы встре­чают пустоту. Это иллю­зор­ный объект, а его «появ­ле­ние» — результат опти­че­ского свойства пара­болы.

Игрушка состоит из двух соос­ных пара­бо­ло­и­дов враще­ния, чаши кото­рых обращены друг к другу, шапочка верх­ней чаши сре­зана. На ниж­ней чаше, в фокусе верх­него пара­бо­ло­ида нахо­дится объект; после отраже­ний в зер­каль­ных стен­ках пара­бо­ло­и­дов в фокусе ниж­него форми­ру­ется изоб­раже­ние.

Исаак Нью­тон заме­тил, что при враще­нии цилин­дри­че­ского сосуда поверх­ность нали­той в него жид­ко­сти при­нимает форму пара­бо­ло­ида, и объяс­нил это явле­ние с помощью най­ден­ных им самим зако­нов.

В наше время этот эффект исполь­зуют при изго­тов­ле­нии больших пара­бо­ли­че­ских зер­кал для теле­скопов — этот спо­соб быст­рее и дешевле, чем клас­си­че­ская шлифовка. А иногда создают и «времен­ные» теле­скопы с жид­ким зер­ка­лом: сосуд с рту­тью вращают только во время про­ве­де­ния наблю­де­ний.

«Пара­бо­ли­че­скими» являются такие альпийские и арк­ти­че­ские цветы, как про­стрел альпийский, бек­ви­чия лед­ни­ко­вая, поляр­ный мак. Благо­даря опти­че­скому свойству пара­болы у таких цве­тов уско­ря­ется созре­ва­ние семян. Ещё одно полез­ное для цве­тов след­ствие их пара­бо­лич­но­сти — при­вле­че­ние насе­комых, кото­рые любят «понежиться» в чаше цветка, а это вли­яет на опы­ле­ние.

Если на пара­боле $y=x^2$ по раз­ные сто­роны от оси $Oy$ взять точки $(-a; a^2)$ и $(b; b^2)$, то соеди­няющий их отре­зок пере­се­чёт ось $Oy$ в точке $(0; ab)$. Пер­вым это отме­тил Август Мёбиус, имя кото­рого носит знаме­ни­тая одно­сто­рон­няя лента.

Можно взгля­нуть на этот факт и с дру­гой сто­роны: через точку $(0;N)$, где $N=ab$ — состав­ное число, про­хо­дит хорда пара­болы опи­сан­ного вида ($a$ и $b$ — нату­раль­ные числа, отлич­ные от 1). А через точку вида $(0;p)$, где $p$ — про­стое число, не про­хо­дит ни одна подоб­ная хорда.

Источник